Olocip, dentro de la iniciativa #StopCorona, ha desarrollado un nuevo modelo que representa de forma más precisa la evolución del COVID-19. El nuevo modelo se fundamenta en el trabajo presentado por el Department of Epidemiology del Imperial College London [1] en el que aplican un modelo SEIR bayesiano que ha sido adaptado para su aplicación en España y sus comunidades autónomas. Tras los cambios, se han incluido nuevas comunidades autónomas a nuestra lista de predicciones.
Diferencias con el modelo anterior
Hasta ahora los resultados presentados por Olocip se han basado en un modelo SEIR determinista. Este modelo formula las transiciones entre estados en forma de ecuaciones diferenciales cuyos parámetros son valores escalares que representan el tiempo esperado de un individuo en cada estado antes de pasar al siguiente.
Sin embargo, los factores clave que determinan la evolución de la pandemia son desconocidos y están envueltos en incertidumbre debido a la dificultad de hacer un seguimiento de todos los casos. Por ello, es más adecuado aplicar un enfoque basado en estadística bayesiana que permita capturar la incertidumbre acerca del valor real de los parámetros del modelo en la dinámica del COVID-19.
En el enfoque bayesiano, las transiciones entre estados se modelan con variables aleatorias que son representadas mediante distribuciones de probabilidad sobre el tiempo que tarda cada individuo en transitar de un estado al siguiente.
Modelo SEIR
La adaptación del modelo SEIR propuesto por Olocip para estimar la evolución de la pandemia en cada comunidad autónoma de España asume que la población se divide en cinco grupos (ver Figura 1): susceptibles de ser contagiados (S: susceptible), en proceso de incubación (E: exposed), contagiados (I: infected), eliminados (R: removed) y fallecidos (D: death). El estado de eliminados (R) representa a las personas curadas, aisladas, o fallecidos, y que en consecuencia ya no pueden contagiar al resto.
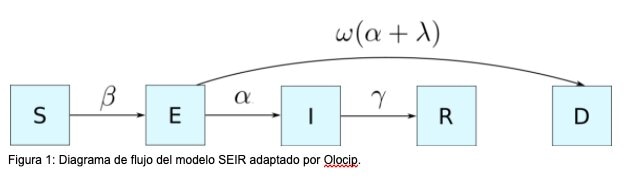
Este proceso se representa mediante un sistema de ecuaciones diferenciales que modelan las transiciones entre estados. Una de las principales diferencias del modelo de Olocip respecto al modelo SEIR estándar se encuentra en la inclusión del estado D que representa al total de fallecidos.
La incorporación de este estado se debe a que una asunción del modelo es que el número de defunciones es un mejor estimador del alcance real de la pandemia que el número de casos confirmados, dado que estos últimos están sesgados por el limitado número de test disponibles.
En las siguientes secciones discutiremos acerca del ajuste del modelo a partir de los datos observados de defunciones. Al incluir este nuevo estado el sistema de ecuaciones diferenciales SEIR pasa a ser el siguiente:

La evolución del sistema está condicionada por dos tipos de parámetros: el estado inicial y los ratios de transición. El estado inicial del sistema viene determinado por el reparto de la población en cada estado al comienzo de la pandemia. Los ratios de transición, representados por las letras griegas en el sistema de ecuaciones, son el inverso del tiempo estimado que un individuo pasa en un estado antes de transitar al estado siguiente. Los ratios de transición son los siguientes:
- β: Número de contagios por cada contagiado (individuos en el estado I) por unidad de tiempo. Al decretar medidas de distanciamiento social el gobierno actúa sobre este parámetro. Nuestro modelo incorpora las intervenciones de acuerdo a la siguiente ecuación [2]:

donde t es un instante de tiempo, t* es el día de las intervenciones y q es un parámetro más a ajustar por el modelo que determina el impacto de la intervención.
- ⍺: Inverso del periodo de incubación.
- ?: Inverso del periodo que un individuo es infeccioso.
- ⍵: Inverso de la tasa de letalidad.
- ƛ: Inverso del periodo que pasa desde que un individuo presenta los primeros síntomas hasta que fallece.
Durante la evolución de una epidemia tanto el estado inicial como los ratios de transición son desconocidos y por lo tanto su valor exacto es una incógnita. Una de las principales limitaciones del modelo SEIR estándar es que es determinista. Esto tiene importantes implicaciones en el conocimiento que puede llegar a aportar y en su precisión.
Para comprender el alcance de la pandemia no es suficiente con conocer el valor esperado de estos condicionantes del sistema de ecuaciones diferenciales, también es importante conocer el grado de certeza que se tiene sobre ellos y ese conocimiento no puede ser adquirido a través de un modelo determinista como el SEIR estándar.
En la siguiente sección discutimos cómo aprovechar el conocimiento experto que ha ido generando la comunidad científica internacional alrededor del SARS-CoV-2. En los modelos propuestos desde Olocip utilizamos estadística bayesiana para combinar esa información con los datos registrados por cada región de España.
Modelo Bayesiano
Durante los últimos meses, se ha generado un importante volumen de trabajos en la literatura científica que investigan el valor de los parámetros que describen el comportamiento del SARS-CoV-2. Por ejemplo, hay bastante consenso en que el tiempo de incubación de la enfermedad dura de media alrededor de cinco días [3,4] o que el tiempo esperado hasta el fallecimiento desde que presentan los primeros síntomas se sitúa alrededor de los 18.5 días [5].
Además, el período infeccioso suele prolongarse entre 4 y 5 días [6]. Sin embargo, factores esenciales para estimar el desarrollo de la pandemia, como el número de reproducción básico (R0), dependen en gran medida de factores sociales, como el número de contactos entre individuos o los desplazamientos entre regiones [7]. Por lo tanto asumir que esté parámetro tomará el mismo valor que en otras regiones del planeta puede suponer introducir importantes errores.
La estadística bayesiana permite modelar el conocimiento previo de los expertos en el campo, o información a priori, en forma de variables aleatorias y actualizarlas de acuerdo a los datos disponibles. Para el problema que nos ocupa, la información a priori se basa en los resultados reportados a nivel internacional en artículos científicos de ámbito epidemiológico. Específicamente, en el modelo SEIR para España hemos utilizado las siguientes distribuciones a priori:
- Periodo de incubación (1/⍺) ~ Gamma(μ = 5.1, σ = 0.86)
- Periodo infeccioso (1/?) ~ Gamma(μ = 4.5, σ = 0.62)
- Periodo desde primeros síntomas hasta fallecimiento (1/ƛ) ~ Gamma(μ = 18.8, σ = 0.45)
También se han incluido como variables a estimar otros factores cruciales para el desarrollo de la pandemia que están muy condicionados a las características de las regiones, como la tasa de transmisión (R0), el número inicial de infectados (I_0N) y el impacto de las intervenciones del gobierno (q) [8]. Debido a que actualmente hay mucha incertidumbre sobre el valor real de estas variables, se les ha asignado distribuciones a priori débiles o poco informativas:
- Tasa de reproducción (R0) ~ Normal(μ = 2.5, σ = 10)
- Número inicial de infectados (I_0N) ~ Normal(μ = 500, σ = 100)
- Impacto de la intervención (q) ~ Gamma(μ = 0.12, σ = 0.1)
Por último, asumimos que el ratio de mortalidad es del 2.3% [7-9].
Mediante inferencia bayesiana [10] se actualiza el conocimiento previo sobre estas variables de acuerdo a lo observado en los datos, dando como resultado una distribución a posteriori que combina las creencias con las observaciones. En este problema, los datos observados son las defunciones recogidas por el Ministerio de Sanidad [11]. Asumimos que esta variable sigue una distribución de Poisson con media D, donde D es el valor del estado que representa a los fallecidos en cada instante temporal. En la Figura 2 se muestran las distribuciones a posteriori de todas las variables utilizadas.
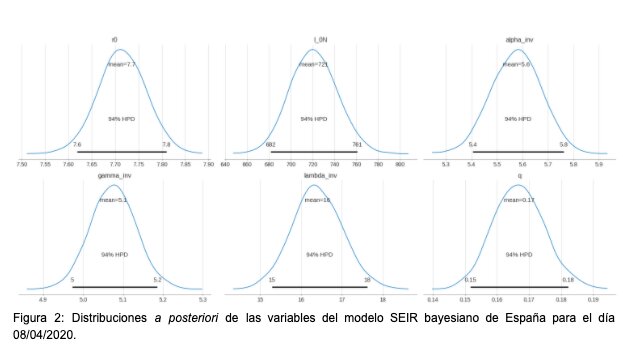
En los modelos autonómicos se han utilizado las mismas distribuciones a priori que en el modelo de España. La única excepción es el impacto de las intervenciones del gobierno, que es una variable muy sensible a errores en los datos de fallecidos de cada región. Esto provoca que en algunas comunidades autónomas los resultados sean poco estables si se utiliza una distribución a priori poco informativa. Para solucionarlo, utilizamos como a priori la distribución a posteriori estimada para España.
En todos los casos, las distribuciones a posteriori de las variables latentes se han aproximado utilizando inferencia variacional [12].
Interpretación de las respuestas del modelo
Los modelos aprendidos se han utilizado para predecir la evolución de los contagios y fallecimientos producidos por el virus SARS-CoV-2 en un horizonte temporal de 30 días que se va actualizando diariamente de acuerdo a los datos que va publicando el Ministerio de Sanidad.
La Figura 3 muestra la evolución esperada de las defunciones en España. En azul se muestran las defunciones acumuladas desde el inicio de la pandemia reportadas oficialmente por el Ministerio de Sanidad, mientras que en rojo se muestran las predicciones del modelo. Adicionalmente, las bandas rojas se corresponden con los intervalos de credibilidad del 95%, que representan la incertidumbre del modelo en sus respuestas. Esta incertidumbre se compone de dos tipos de error, epistémico y aleatorio. En nuestro modelo, el error epistémico viene dado por la incertidumbre en el valor de las variables latentes, y se podría reducir incrementando el volumen de los datos. El error aleatorio es inherente a las observaciones y es irreducible a no ser que se aumente la precisión en la recogida de datos o se utilice un modelo que refleje mejor la realidad. Analizando la gráfica se puede observar que el modelo estima que cuando se estabilice la pandemia el número acumulado de fallecidos en España será próximo a 17.800, e inferior a 22.100 con un 95% de probabilidad.
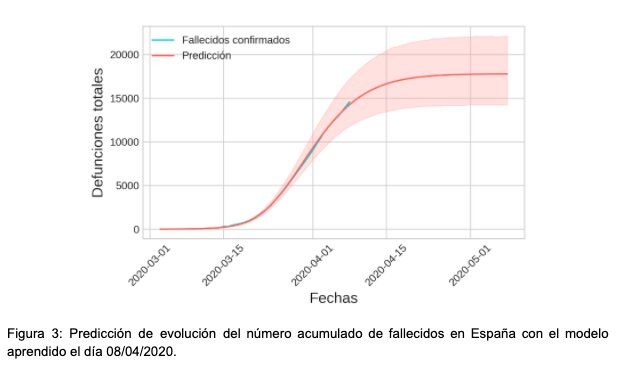
La figura 4 muestra la evolución esperada de los contagios en España. Para cada fecha se muestra el número de personas infectadas con el virus y en disposición de contagiar a la población susceptible. Las estimaciones del modelo se muestran en rojo, mientras que los datos oficiales se muestran en azul. Se puede observar que las predicciones se separan de los datos oficiales por un amplio margen. Esto se debe a que los contagios reportados oficialmente están limitados al número de tests disponibles, mientras que el modelo basa sus predicciones de contagiados en la evolución del número de defunciones. En la gráfica se puede observar que de acuerdo al modelo, el día 3 de abril es la fecha donde es más probable que se produjera el pico, y con un 95% de probabilidad se estima que el número de personas que estaban contagiadas en esa fecha se encontraba entre 545.000 y 810.000 individuos.
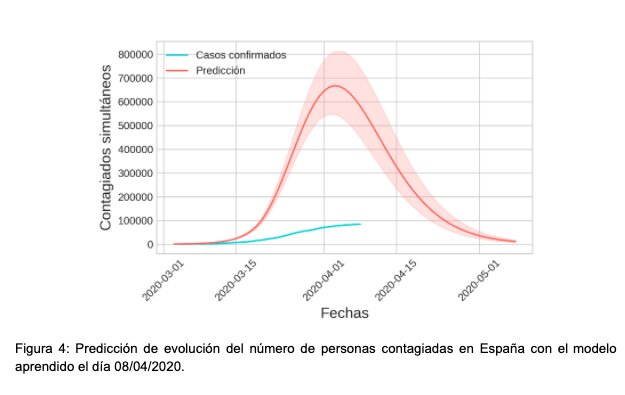
Conclusiones
El enfoque propuesto en este documento ofrece muchas posibilidades. A partir de su aplicación se puede predecir la evolución de las defunciones causadas por el coronavirus, estimar el valor real de contagios y predecir su evolución en las distintas regiones del país. Al abordar el desarrollo del modelo de acuerdo a un enfoque bayesiano este es capaz de representar la incertidumbre en las salidas del modelo en forma de intervalos de credibilidad. Con ello es posible anticiparse al problema de la movilización de recursos, como son por ejemplo los respiradores artificiales, los test o las mascarillas, que pueden destinarse a donde sean más necesarios.
En el futuro planeamos utilizar el modelo para simular nuevas intervenciones del gobierno y estimar cómo afectarían las distintas medidas a la evolución de la pandemia. Esto nos permitirá identificar los momentos más propicios para empezar a relajar las medidas de distanciamiento social.
Además, la metodología aplicada es extrapolable a otros países en los que la pandemia lleve menos tiempo activa y por tanto haya poca información. Para estos países se podrían aprovechar los parámetros a posteriori aprendidos para España o alguna de las regiones donde el virus tiene un mayor recorrido para introducirlos como información a priori con el fin de proporcionar respuestas inmediatamente.
Referencias
[2]Lekone, P. E. & Finkenstädt, B. F. (2006). Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics, 62(4), 1170-1177.
[3]Kucharski, A. J., Russell, T. W., Diamond, C., Liu, Y., Edmunds, J., Funk, S. & Davies, N. (2020). Early dynamics of transmission and control of COVID-19: A mathematical modelling study. The Lancet Infectious Diseases.
[4]Backer, J. A., Klinkenberg, D., & Wallinga, J. (2020). Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eurosurveillance, 25(5).
[5]Zhou, F., Yu, T., Du, R., Fan, G., Liu, Y., Liu, Z. & Guan, L. (2020). Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. The Lancet.
[6] Anderson, R. M., Heesterbeek, H., Klinkenberg, D., & Hollingsworth, T. D. (2020). How will country-based mitigation measures influence the course of the COVID-19 epidemic?. The Lancet, 395(10228), 931-934.
[6]Prem, K., Liu, Y., Russell, T., Kucharski, A. J., Eggo, R. M., Davies, N. & Klepac, P. (2020). The effect of control strategies that reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China. The Lancet.
[7]Xu, Z., Shi, L., Wang, Y., Zhang, J., Huang, L., Zhang, C. & Tai, Y. (2020). Pathological findings of COVID-19 associated with acute respiratory distress syndrome. The Lancet Respiratory Medicine, 8(4), 420-422.
[8]Chen, Y., & Li, L. (2020). SARS-CoV-2: virus dynamics and host response. The Lancet Infectious Diseases.
[9]Onder, G., Rezza, G., & Brusaferro, S. (2020). Case-fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA.
[10]Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A. & Rubin, D. B. (2013). Bayesian Data Analysis. CRC Press.
[12] Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., & Blei, D. M. (2017). Automatic differentiation variational inference. The Journal of Machine Learning Research, 18(1), 430-474.



